I came across a post from Emily Willingham the other day: "Is a PhD required for Good Science Writing?". As a science writer with a science PhD, her answer is: is it not required, and it can often be an impediment. I saw a similar sentiment echoed once by Lee Gutkind, the founder and editor of the journal Creative Nonfiction. I don't remember exactly what he wrote, but it was something to the effect that scientists are exactly the wrong people to produce literary, accessible writing about matters scientific.

Photo: John Mount
I don't agree with Gutkind's point, but I can see where it comes from. Academic writing has a reputation for being deliberately obscure and prolix, jargonistic. Very few people read journal papers for fun (well, except me, but I'm weird). On the other hand, a science writer with a PhD has been trained for critical thinking, and should have a nose for bullpucky, even outside their field of expertise. This can come in handy when writing about medical research or controversial new scientific findings. Any scientist -- any person -- is going to hype up their work. It's the writer's job to see through that hype.
I'm not a science writer in the sense that Dr. Willingham is. I write statistics and data science articles (blog posts) for non-statisticians. Generally, the audience that I write for is professionally interested in the topic, but aren't necessarily experts at it. And as a writer, many of my concerns are the same as those of a popular science writer.
I want to cut through the bullpucky. I want you, the reader, to come away understanding something you thought you didn't -- or even couldn't -- understand. I want you, the analyst or data science practitioner, to understand your tools well enough to innovate, not just use them blindly. And if I'm writing about one of my innovations, I want you to understand it well enough to possibly use it, not just be awed at my supposed brilliance.
I don't do these things perfectly; but in the process of trying, and of reading other writers with similar objectives, I've figured out a few things.
It's not a research paper; don't write it like a research paper.
To the outsider (and sometimes, to the insider), academic writing is a giant exercise in gamesmanship. The goals are to demonstrate that you are smarter than your peers, and your research is innovative and novel. Those goals impede clarity; after all, if it's hard to read, it must be difficult material, and you must be one smart cookie.
When you are writing for the public, or for the practitioner, you usually aren't writing about something you invented. This frees you from the pressure of appearing novel, and the topic doesn't have to seem profound. You don't have to try to look smart, either. By definition, you know something the reader doesn't -- and if you can explain it so that it seems obvious in hindsight, you actually look that much more clever.
Channel your inner undergrad.
This is related to the first point. Your readers are not your research peers, but they aren't stupid, either. They just have a different set of expertise. They won't know all the acronyms or the standard symbology, they won't know all the terminology or all the logic shortcuts (and occasional sloppy misuse of terminology) that people in the field are accustomed to. They are, however, motivated to learn the subject matter. It's your job to make it all make sense.
This is where I have an advantage in writing about statistics: my PhD isn't in statistics. I learned it after I started working, because I had to. I remember a good deal of frustration with the general presentations of standard material given in textbooks. And I can remember even more frustrations with the "insider" style of writing in research papers -- often a lot of hard work for not a lot of reward. The Statistics to English series of blog posts arose from that experience. It doesn't have to be that hard.
Explain everything. If you are going to talk about p-values, for example, then define what they are; define significance, or at least point to a readable reference. Don't expect your readers to know that π means "vector of probabilities" and not "the area of a unit radius circle." In any technical field, a clear explanation of definitions -- especially terms and symbols that are used differently in different fields, like "entropy" or "likelihood" -- is worth a lot. It may not seem like much, but believe me, your readers will thank you.
If an explanation helps make sense of a concept to you, it will probably make sense to someone else.
... and therefore, it will be helpful to someone, if not everyone. A related point to this is that parroting the textbook or research paper explanations is not always helpful, no matter how official or technical it sounds.
An example: the definition of likelihood (or likelihood function) from The Cambridge Dictionary of Statistics is as follows:
The probability of a set of observations given the value of some parameter or set of parameters.
The dictionary goes on to give an example, the likelihood of a random sample of n observations, x1,..x2,...xn with probability distribution f(x,θ):
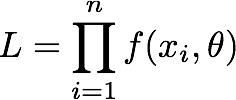
This makes perfect sense, from a 50,000 foot point of view, especially if you are in the habit of thinking statistically. But what if you aren't? Or if you want to actually calculate a specific likelihood for a specific purpose? Like the person who asked a question about likelihood versus probability here. This person received several excellent answers, most of which were elaborations of the Cambridge definition, with variations on how the likelihood formula was written. This seems to have helped the original questioner; but I can tell you that back in the days when I was struggling to learn these concepts, it wouldn't have helped me. I learn by concrete examples. Like this (borrowed from one of the answers at the link):
I have an unfair coin, and I think that the probability that it will land heads is p. I flip the coin n times, and I record whether it lands heads (x_i=1), or whether it lands tails (x_i=0). The likelihood of observing my series of coin flips, given that I have guessed probability p correctly is:
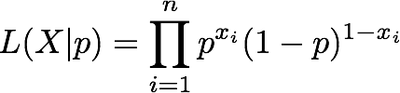
Here, I'm using the notation L(x|p) to emphasize that the likelihood of the set of observations X is dependent on my "model" -- the estimate for p. If the likelihood is high, I have guessed p correctly; if it is low, I need to re-estimate p.
We can generalize this to any set of observations X that lead to a binary outcome, and any model for the probability, P(x).
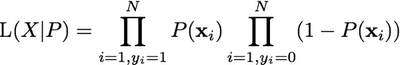
Again, if the likelihood isn't high, then we need to adjust our model P(x), probably by tweaking some parameter or parameters θ within the model. This leads us back to the original Cambridge definition.
My formula is not as general as the Cambridge formula (or the formulas given by the people who answered the question in my link above), and it may still not be clear enough for everyone. Still, it helped me; this is the formula I use to explain the use of likelihood in deriving logistic regression. Judging by Win-Vector's blog stats, it helps other people out there, too.
Few things are "obvious."
But after all, the most successful device in mathmanship is to leave out one or two pages of calculations and for them substitute the word "hence," followed by a colon. This is guaranteed to hold the reader for a couple of days figuring out how you got hither from hence. Even more effective is to use "obviously" instead of "hence," since no reader is likely to show his ignorance by seeking help in elucidating anything that is obvious. This succeeds not only in frustrating him but also in bringing him down with an inferiority complex, one of the prime desiderata of the art.
-- Nicolas Vanserg, "Mathmanship" (1958). Originally published in American Scientist, collected in A Stress Analysis of a Strapless Evening Gown: Essays for a Scientific Age. Sorry, couldn't find the essay online.
If it is "obvious" enough to be explained concisely, then explain it. If the calculation or derivation is short, then spell it out. Otherwise, use another phrase like "it happens to be the case", or "it can be shown," with references -- or at least cop to the fact that it's a messy calculation. Some people will complain about how long your posts are; but there will also be an army of students and other novices who will be grateful to you, because they finally "get it."
And finally:
No matter how hard you try, someone will think you stink. Let it go.
Even if you don't write your article like a research paper, someone out there will read it (or criticize it) as if it were. If you try to define every concept and explain every chain of reasoning, you will get snarky "TLDR" (too long, didn't read) comments, or comments to the effect that it was a lot of reading for a point that was "obvious." If you express an opinion, no matter how mildly or with any number of qualifications (for example, my colleague John Mount's article on why he dislikes dynamic typing), you will get sarcastic comments from those who hold the opposite opinion, on why you are just wrong, or why the issues you point out are your fault, not (e.g.) dynamic typing's fault. You will get people hurling back at you points that you already addressed in the post.
So fine, some people don't read (or are too impatient or closed-minded to read); they aren't your readers. Just let it go and move on.
Being the concrete-minded person that I am, these points are addressed to my specific situation; but I hope that they are useful to other science writers and technical writers as well. I'm sure that I've violated many of these points in my own writing; hopefully the more I keep at it, the better my writing gets.