The Wine Thief Problem

This puzzle is again from Dudeney's "The Worlds Best Puzzles", in the December 1908 Strand Magazine. It's another one from Bachet, who gave us The Four Weights Problem.

A wine connoisseur has a wine-bin of eight compartments, containing 60 bottles of wine, as shown below:

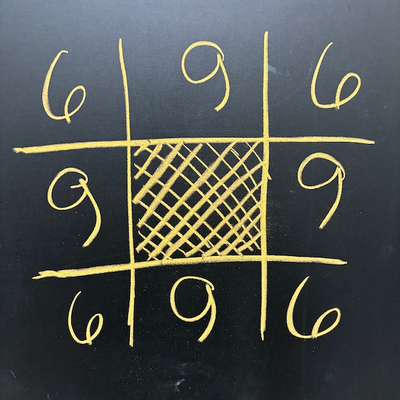
3x3 square of numbers, with a in the corners and b in the middle edges, center blank

His dishonest employee steals 4 bottles and rearranges the remainder. The connoisseur notices that the bottles have been rearranged, but on counting, he notes that there are still 21 bottles on each side, so he decides that everything is fine.

The employee, emboldened, steals 4 more---and then another 4, and then another 4, for a total of 16 bottles. Each time, he rearranges the remaining bottles so that there are 21 bottles on each side.

How did the employee arrange the bottles after each theft, so that the connoisseur never noticed?

Yes, the connoisseur was amazingly unobservant, or amazingly naive, but let's just roll with it. Solution after Chirico's The Mathematicians.

Allegorical sketch of beings in a courtyard, both made of mathematical instruments

The Mathematicians (1917)
Artist: Giorgio de Chirico. Source: WikiArt

Solution #

A little thought should convince you that there is a symmetric solution: the thief steals a bottle from each center bin and then moves another bottle from the center into a corner bin appropriately. So the wine bins always look like this:

for some values of $a$ and $b$ . Let's set that up algebraically.

$2 a + b = 21$ (the sum of each side is 21)
$4 a + 4 b = w$ , where $w$ is the number of wine bottles remaining.

Look familiar? Since $a$ and $b$ , and $w$ are all nonnegative integers, and so are the coefficients, this is another system of Diophantine equations, similar to 100 Bushels of Corn.

We know what the $w$ are from the problem statement: [60, 56, 52, 48, 44].Define $n = w / 4$ to make things easier (note $n$ is also a nonnegative integer). Then a bit of algebra gives you:

\begin{aligned} a & = 21 - n \\ b & = 2 n - 21 \\ w & = 4 n \\ n & \in 15 : 11 \end{aligned}

(I'm counting $n$ backwards because that's the progression of the puzzle).

Notice that this follows the general form of Diophantine system solutions that John Mount describes here: we've established the linear structure, set up the correct modular relations and parameterization, and found the integral endpoints that enforce the sign constraints. Of course, in this case, the endpoints were pretty much given to us.

Now we can just fill in the table of cases. I'll even do this one by hand.

wine bottles	n	a (corner)	b (center)
60	15	6	9
56	14	7	7
52	13	8	5
48	12	9	3
44	11	10	1

And after this, of course, even our oblivious connoisseur won't be able to avoid noticing his losses.

"Half-symmetric" Solutions #

There is another set of solutions, where instead of all the corners having the same number of bottles, the diagonally opposite corners do:

3x3 square of numbers, with a in the top left and bottom right corners, c in the other corners, and b in the middle edges, center blank

This will (with some algebra) give the system:

\begin{aligned} a + c & = 42 - n \\ b & = n - 21 \\ w & = 2 n \\ n & \in 30 : 22 \end{aligned}

which in turn produces the table:

wine bottles	n	a+c	b
60	30	12	9
56	28	14	7
52	26	16	5
48	24	18	3
44	22	20	1

The point is that any combination of $a$ and $c$ that produces the correct sum will work. If $a = c$ , then we have the completely symmetric solution above.

So the thief, if he wanted to, could mix up the arrangements, to (maybe) make the thefts less apparent.